SIMPLE LIFTING MACHINES
LIFTING MACHINES
-
SIMPLE PULLEY
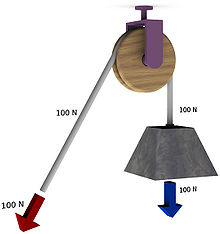
A simple pulley is a wheel of metal or wood, with a groove around its circumference, to receive rope or chain. The pulley rotates freely about its axle, which passes through its centre and is perpendicular to its surface plane. This axle is supported by a metal or a wooden frame, called block. Following assumptions are made in the study of pulley system:
- The weight of the pulley block is small as compared to the weight to be lifted, and thus may be neglected in calculations.
- The friction between the pulley surface and the string is negligible, and thus the tension in the two sides of the rope, passing round the pulley, may be taken to be equal.
A little consideration will show, that in a simple pulley, its mechanical advantage as well as velocity ratio is 1 under the assumed conditions mentioned above. Simple pulleys are generally used to change the direction of the applied effort.
When several pulleys are arranged, it is possible to obtain a mechanical advantage. The three systems of pulleys, which are commonly used are:
- First system of pulleys.
- Second system of pulleys.
- Third system of pulleys.
-
FIRST SYSTEM OF PULLEYS
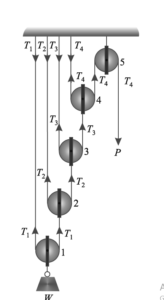
In this system, the pulleys are so arranged that there are as many strings as there are pulleys. The end of each string is fastened to a rigid ceiling; while the other end passing round the bottom periphery of the pulley, is fastened to the next higher pulley. The load is attached to the bottom-most pulley ; whereas the effort is applied to the far end of the string passing round the last pulley. Another pulley (no. 5) is used just to change the direction of the effort. The velocity ratio of the system may be obtained by considering a unit motion of the load.
In this case, let the weight W be raised by x metres. Since the loads is supported on both sides of the string, thus this slackness of x metres will have to be taken up by the pulley 2. If the relative position of the pulley 2, with respect to the pulley 1, is to remain undisturbed, then the pulley 2 should move upwards through a distance of 2x metres.
Now this upward movement of pulley 2 through a distance of 2x metres will cause a total slackness of 2 × (2x) = 22x metres in the string, which has to be taken up by the pulley 3.
First System of Pulleys
Thus the pulley 3 should move upwards through a distance of 22x metres, thus causing a slackness of 2 × (22x) = 23x in the string passing round the pulley 4.
Thus the pulley 4 should move upwards through a distance of 23x metres causing a slackness of 2 × (23x) = 24x meters, which must be taken up by the free end of the string to which the effort is applied. Thus the effort must move through a distance of 24x metres.
Let P be the effort required to lift a load W.
In equilibrium condition
For pulley 1, we have 2T1 = W ∴ T1 = [frac up=”W” down=”2″]
For pulley 2, we have 2T2 = W ∴ T2 = [frac up=”T1” down=”2″] = [frac up=”W” down=”22“]
For pulley 3, we have 2T3 = W ∴ T3 = [frac up=”T2” down=”2″] = [frac up=”W” down=”23“]
For pulley 2, we have 2T4 = W ∴ T4 = [frac up=”T3” down=”2″] = [frac up=”W” down=”24“]
Now T4 = P (Considering the equilibrium of pulley 4)
∴ P = [frac up=”W” down=”24“]
Hence, if ‘n’ number of pulleys are in the system then P = [frac up=”W” down=”2n“]
∴ M.A. = 2n
Since it is assumed that efficiency of the system is 100%, therefore Mechanical Advantage = Velocity Ratio
∴ V.R. = 2n
-
SECOND SYSTEM OF PULLEYS
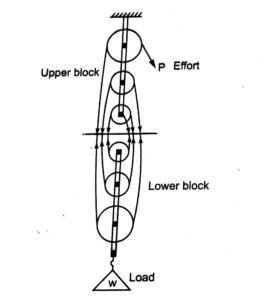
Second system of pulleys contains two blocks, one upper and the other lower, both carrying either equal number of pulleys or the upper block may have one pulley more than the lower one. In both the cases, the upper block is fixed and the lower one is movable. There is only one string, which passes round all the pulleys one end of which is fixed to the upper block (when both the blocks have the same no. of pulleys) or to the lower block (when the upper block has one pulley more than the lower one). The other end of the string is free and the effort is applied to this free end. In both the cases the load is attached to lower block.
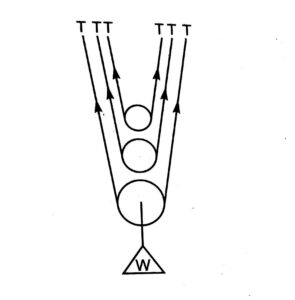
For equilibrium, we have
W = 6T
Since, T = P
W = 6P
[frac up=”W” down=”P”] = 6 M.A.
For 100% efficiency,
M.A. = V.R.
V.R. = 6
In general if there are n number of pulleys in the system, then
V.R. = n
-
THIRD SYSTEM OF PULLEYS
In this system, like the first system of pulleys, the pulleys are arranged in such a way that there are as many strings as
there are pulleys. One end of each string is fixed to a block, to which the load is attached. The other end of each
string, passing round the upper periphery of the pulley, is fastened to the next lower pulley.
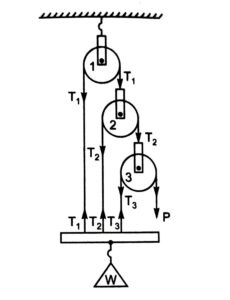
Let T1, T2, T3 be the tensions in the strings in pulley 1, 2, 3 respectively. Considering the equilibrium of the system.
T1 + T2 + T3 = W
Again P = T3
and considering the equilibrium of individual pulleys we get,
T2 = 2T3 = 2P
T1 = 2T2 = 22T3
T1 = 22P
Putting the values of T1, T2, T3, we get,
W = (22P + 2P +P)
W = P(4 + 2 + 1)
W = 7P
W = (23 – 1) P
If we have n number of pulleys in the system then,
W = (2n – 1) P
[frac up=”W” down=”P”] = M.A. = (2n – 1)
For ideal machine efficiency = 100%, i.e. V.R. = M.A.
∴ V.R. = (2n – 1)
RELATED VIDEOS FOR SYSTEM OF PULLEYS:
