SIMPLE LIFTING MACHINES

 

 

FRICTION IN A MACHINE

There are always some losses in every machine and these losses are mainly due to friction. The machine loss or machine friction may be expressed either on the effort side or on the load side. When expressed on the effort side, the friction may be defined as an additional effort required to overcome the frictional forces. But when expressed on the load side, the friction may be defined as the additional load that can be lifted.

Let,

W = Actual load lifted
W_i = Ideal load lifted (Wi > W)
P = Actual effort required to lift a load
P_i = Ideal effort required to lift a load (Pi < P)
L_P = Loss of effort due to friction
L_W = Loss of load due to friction

∴ L_P = P – P_i         …(1)
∴ L_W = W_i – W   …(2)

For an ideal machine,

M.A. = V.R.

[frac up=”W” down=”P_i“] = V.R.

P_i = [frac up=”W” down=”V.R.”]   …(3)

 

Substituting the value of in P_i equation 1

L_P = P – [frac up=”W” down=”V.R.”]   …(4)

 

For an ideal machine,

M.A. = V.R.
[frac up=”W_i” down=”P”] = V.R.

W_i = V.R. x P   …(5)

 

Substituting the value of in W_i equation 2

L_W = V.R. X (P – W)   …(6)

 

Dividing both sides of equation (6) by V.R.

[frac up=”L_W” down=”V.R.”] = P – [frac up=”W” down=”V.R.”]

 

From equations 4 and 7, we get

[frac up=”L_W” down=”V.R.”] = L_P

∴ L_W =  L_P x V.R

 

REVERSIBLE MACHINE AND IRREVERSIBLE MACHINE

When the machine is capable of doing work in the reverse direction due to its load, as the effort is totally removed, the machine is said to be reversible machine.

Let P be the effort required to raise a load W. If P is removed W will fall down. Then the machine is called reversible machine.

 

When the machine is not capable of doing any work in the reverse direction, after the effort is removed, then the machine is called an irreversible or self-locking machine.

Let P be the effort required to lift a load W. When P is removed W will not fall down then this type of machine is self-locking or irreversible machine.

 

CONDITION FOR REVERSIBILITY OF A MACHINE (REVERSIBLE MACHINE)

The condition for reversibility of a machine can be found as follow:

Let,

W = Load lifted by the machine,
P = Effort required to lift the load,
y = Distance moved by the effort, in lifting the load
x = Distance moved by the load.

We also know that,

Input = Effort x Distance moved by the effort = P x y

Output = Load x Distance moved by the load = W x x

and

Frictional losses in the machine = Input – Output = Py – Wx

In a reversible machine, the machine friction is less than the output of the machine.

∴ (Py – Wx) < Wx

Py < 2 Wx

[frac up=”1″ down=”2″] < [frac up=”Wx” down=”Py”]

[frac up=”W/P” down=”y/x”] > [frac up=”1″ down=”2″]

[frac up=”M.A” down=”V.R”] > [frac up=”1″ down=”2″]

∴ Efficiency > [frac up=”1″ down=”2″] > 50%

Hence the condition for a machine, to be reversible, is that its efficiency should be more than 50%.

 

LAW OF MACHINE

The relationship between the effort required in a machine and the load is called the Law of Machine.

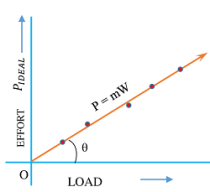
Thus for any machine, if we record the various efforts required to raise the corresponding loads, and plot a graph between effort and load, we shall get a straight line.

For an ideal machine the straight line will pass through the origin.

 

 

 

For an actual machine straight line will have an intercept at C. The intercept C is the amount of effort required by the machine to overcome the friction.

 

 

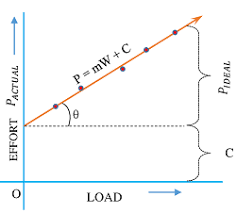
Mathematically, the law of a lifting machine is given by the relation :

P = mW + C

where,

P = Effort applied to lift the load,
m = A constant (called coefficient of friction) which is equal to the slope of the line,
W = Load lifted, and
C = Another constant, which represents the machine friction

 

 

 

RELATED VIDEOS:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

For More Information:- CLICK HERE