FRICTION
EQUILIBRIUM OF BODY ON INCLINED PLANE:
Any system of forces that keeps the body at rest on an inclined plane is said to be equilibrium of body on an inclined plane. Equilibrium is applicable to those systems of forces whose resultant action is zero.
CASE 1: Force Acting Along The Inclined Plane:
1(a) : When the Body is just on the point of motion down the plane:
Consider a block of weight W is kept on an inclined plane having angle of inclination α with horizontal. The block is just at the point of sliding downward. The force acting on the block, which keep it in equilibrium are:
- Weight of the block, W acting vertically downward.
- Applied force, P
- Frictional force, F acting upward along the plane
- Normal reaction, R
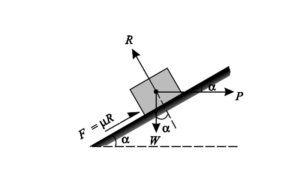
Resolving the forces perpendicular to the inclined plane
R = W cos α
Resolving the forces parallel to the plane
P + F = W sin α
P + μR = W sin α
P + μ.W cos α = W sin α
P = W sin α – μ.W cos α
P = W ( sin α – μ cos α)
P = W ( sin α – tan Φ.cos α)
P = W { sin α – [frac up=”sin Φ” down=”cos Φ”] cos α}
P = W [frac up=”( sin α. cos Φ – sin Φ. cos α)” down=”cos Φ”]
P = W. [frac up=”sin (α – Φ)” down=”cos Φ”]
1(b) : When the Body is just on the point of motion up the plane:
Consider a block of weight W is kept on an inclined plane having angle of inclination α with horizontal. The block is just at the point of sliding upward. The force acting on the block, which keep it in equilibrium are:
- Weight of the block, W acting vertically downward.
- Applied force, P
- Frictional force, F acting downward along the plane
- Normal reaction, R
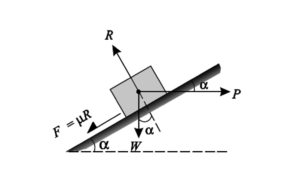
Resolving the forces perpendicular to the inclined plane
R = W cos α
Resolving the forces parallel to the plane
P = W sin α + F
P = W sin α + μR
P= W sin α + μ.W cos α
P = W sin α + μ.W cos α
P = W ( sin α + μ cos α)
P = W ( sin α – tan Φ.cos α)
P = W { sin α + (sin Φ/ cos Φ) cos α}
P = W( sin α. cos Φ + sin Φ. cos α)/ cos Φ
P = W. sin (α + Φ)/ cos Φ
CASE 2: Force Acting Horizontally:
2(a) : When the Body is just on the point of motion down the plane:
Consider a block of weight W is kept on an inclined plane having angle of inclination α with horizontal. The block is just at the point of sliding downward. The force acting on the block, which keep it in equilibrium are:
- Weight of the block, W acting vertically downward.
- Applied force, P acting horizontally
- Frictional force, F acting upward along the plane
- Normal reaction, R
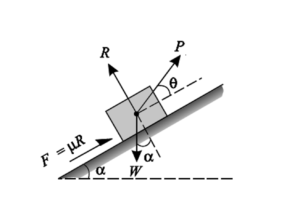
Resolving the forces perpendicular to the inclined plane
R = W cos α + P sin α
Resolving the forces parallel to the plane
P cos α + F = W sin α
P cos α + μR = W sin α
μR = W sin α – P cos α
Putting the value of R, we get
μ(W cos α + P sin α) = W sin α – P cos α
μW cos α + μP sin α = W sin α – P cos α
P cos α + μP sin α = W sin α – μW cos α
P (cos α + μ sin α) = W (sin α – μcos α)
P (cos α + tan Φ.sin α) = W (sin α – tan Φ.cos α)
P {cos α + [frac up=”sin Φ” down=”cos Φ”] sin α} = W {sin α – [frac up=”sin Φ” down=”cos Φ”] cos α}
P(cos α.cos Φ + sin α.sin Φ} = W {sin α.cos Φ – cos α.sin Φ}
P cos (α – Φ)=W sin(α – Φ)
P = W. [frac up=”sin(α – Φ)” down=”cos (α – Φ)”]
P = W tan (α – Φ)
2(b) : When the Body is just on the point of motion up the plane:
Consider a block of weight W is kept on an inclined plane having angle of inclination α with horizontal. The block is just at the point of sliding upward. The force acting on the block, which keep it in equilibrium are:
- Weight of the block, W acting vertically downward.
- Applied force, P acting horizontally
- Frictional force, F acting downward along the plane
- Normal reaction, R
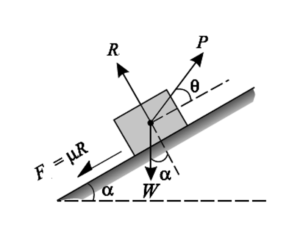
Resolving the forces perpendicular to the inclined plane
R = W cos α + P sin α
Resolving the forces parallel to the plane
P cos α = F + W sin α
P cos α = μR + W sin α
μR = P cos α – W sin α
Putting the value of R, we get
μ(W cos α + P sin α) = P cos α – W sin α
μW cos α + μP sin α = P cos α – W sin α
P cos α – μP sin α = W sin α + μW cos α
P (cos α – μ sin α) = W (sin α + μcos α)
P (cos α – tan Φ.sin α) = W (sin α + tan Φ.cos α)
P {cos α – [frac up=”sin Φ” down=”cos Φ”] sin α} = W {sin α + [frac up=”sin Φ” down=”cos Φ”] cos α}
P(cos α.cos Φ – sin α.sin Φ} = W {sin α.cos Φ + cos α.sin Φ}
P cos (α + Φ)=W sin(α + Φ)
P = W. [frac up=”sin(α + Φ)” down=”cos (α + Φ)”]
P = W tan (α + Φ)
RELATED VIDEOS:
