STRAIN ENERGY:
When an elastic material is deformed under load, work is done by the applied load against the internal resisting forces induced in the material. The work done by the load in straining the body is stored within the strained material in the form of Strain Energy.
Thus it is defined as the energy absorbed by a member within the elastic region.
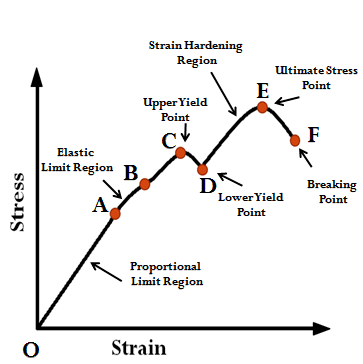
- RESILIENCE is defined as the energy absorbed by a member within the elastic region.
- TOUGHNESS is defined as the energy absorbed by a member just before its fracture.
- It is a form of energy and is recoverable without loss on removal of the load but it is true only when the material is strained only up to the elastic limit. However, if the elastic limit is exceeded, the work done during non-elastic strain is spent in overcoming the cohesion of the particles of the material, causing them to slide one over the another and the energy expanded appears as heat in the material strained.
- S.I. UNIT -: N – m (Joules)
STRAIN ENERGY IN SIMPLE TENSION AND COMPRESSION:
Let us take the case of a bar of cross-sectional area A and length L and subjected to a load P. Suppose this extends the bar by an amount δl and produces a maximum stress σ.
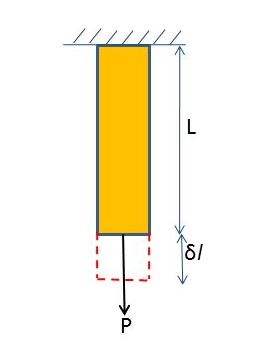
When the load (P) is applied, internal resistance force (F) is set up in the bar and this is stored up in the form of strain energy.
As the load P is increased gradually, the resistance (F = P) is increased gradually.
Am increment δP1 in load results in corresponding incremental deformation δl1.
∴ Work Done by load(External Energy), P = [frac up=”1″ down=”2″] . P . δl —– (equation 1)
Strain Energy (Internal Energy), U = Work Done by Internal Resistance Force (F) —– (equation 2)
Under static equilibrium condition
Strain Energy (U) = Work Done by Internal Resistance Force (F) = Work Done by load (P)
∴ U = [frac up=”1″ down=”2″] . P . δl
U = [frac up=”1″ down=”2″] . P . [frac up=”PL” down=”AE”]
U = [frac up=”P2L” down=”2AE”]
U = [frac up=”P2L” down=”2AE”] . [frac up=”A” down=”A”]
U = [frac up=”P2LA” down=”2A2E”]
U = [frac up=”σ2AL” down=”2E”]
U = [frac up=”1″ down=”2″] . σ . [frac up=”σ” down=”E”] . AL
U = [frac up=”1″ down=”2″] . σ . εlong . AL
Conditions to be met for using the above mentioned equations:
- Static Load
- Prismatic Bar
- Pure Axial Loading
- Same Material
- Elastic Deformation
INELASTIC STRAIN ENERGY:
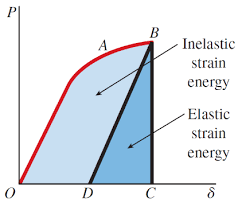
- When the bar is stretched only up to the elastic limit, the deformation will disappear completely on the removal of the load and there will be no residual deformation. The strain energy stored in the bar is then known as ELASTIC STRAIN ENERGY.
- If the bar is loaded up to the point B, beyond the elastic limit (A), the deformation will not disappear completely on the removal of the load. During loading, the work done is equal to the area under the curve OABCDO.
- When the load is removed, the load deflection follows the line BD and a permanent deformation OD remains.
- OD is known as the permanent set. Hence the recovered strain energy is only the one represented by the triangle BCD. The recoverable energy is known as Elastic Strain Energy while the area OABDO represents the Inelastic Strain Energy which is lost in the process of permanent deforming the bar.
-
RESILIENCE:
The strain energy per unit volume of the material is known as Resilience.
It will represent the area of stress-strain curve up to the elastic limit and if the material is treated as elastic up to the yield point than it will represent the area of stress-strain curve up to yield point.
-
PROOF RESILIENCE:
It is the maximum energy absorbed by a component within the Elastic Region.
-
MODULUS OF RESILIENCE:
It is the maximum energy absorbed by a component per unit volume within the Elastic Region.
Modulus of Resilience = [frac up=”Resilience” down=”Volume”]
-
TOUGHNESS:
It is the strain energy absorbed by a component just before its fracture. It represents the area of stress-strain curve up to the fracture point or it represents the total area of the stress-strain curve.
-
MODULUS OF TOUGHNESS:
It is the maximum energy absorbed by a component per unit volume up to fracture point.
Modulus of Toughness = [frac up=”Toughness” down=”Volume”]
STRESSES DUE TO DIFFERENT TYPES OF LOADS:
- STATIC LOAD: The load whose magnitude and direction remains constant.
- GRADUALLY APPLIED LOAD: A body is said to be acted upon by a gradually applied load if the load increases from zero and reaches its final value stepwise.
For More Information:- CLICK HERE