STRENGTH OF MATERIALS- Stresses and Strains

STRESS:

When a body is acted upon by some load or external force, it undergoes deformation which increases gradually. During this deformation, the material of the body resists the tendency of the load to deform the body and when the influence of the load is taken over by the internal resistance of the material of the body, it becomes stable. This internal resistance which the body offers to meet with the load is called stress or stresses.

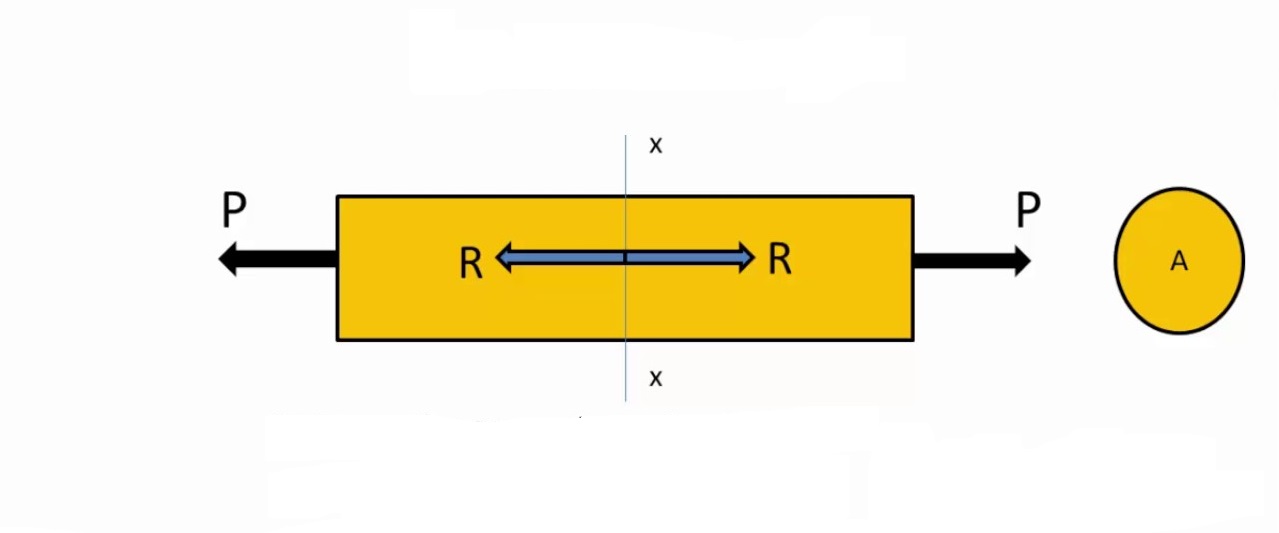
Consider a prismatic bar subjected to axial forces at the ends. A section is x-x taken in order to know the internal stresses produced in the bar. If we consider the equilibrium of right part taken as free body, the internal resistance or the stress offered by the molecules against the external force may be assumed to be uniformly distributed.

Therefore, Internal Resistance = Stress, σ = [frac up=”Load” down=”Area”] = [frac up=”P” down=”A”]

In order for the equation “σ = [frac up=”P” down=”A”]” to be valid, the stress must be uniformly distributed over the cross-section of the bar. This condition is realized if the axial force P acts through the centroid of the cross-sectional area. When the load “P” does not act through the centroid, bending of the bar will result.

TYPES OF STRESSES:

Normal Stresses
Shear Stresses
Bending Stresses
Twisting Stresses
Bearing Stresses

NORMAL STRESSES:

When a stress acts in a direction perpendicular to the cut surface, it is known as Normal Stress or Direct Stress.
Normal Stresses are of two types:

(a) Tensile Stress (b) Compressive Stress

TENSILE STRESS:

When a body is stretched by the force P, the resulting stresses are called tensile stresses. Thus tensile stress exists between two parts of a body when each draws the other towards itself.

COMPRESSIVE STRESS:

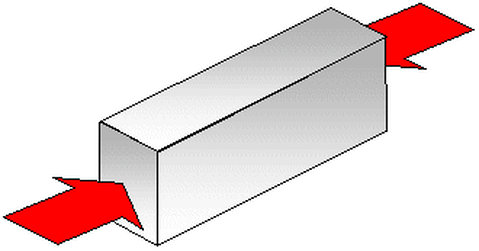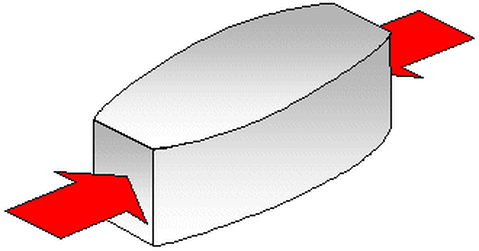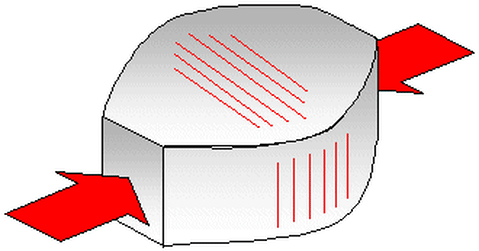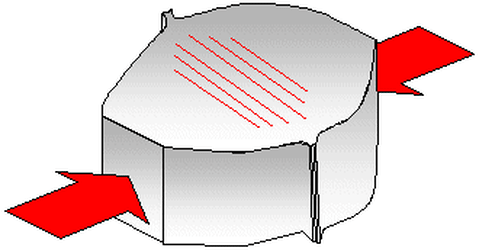
If the forces are reversed in direction, causing the body to be compresses, we obtain compressive stresses. Thus, compressive stress exist between two parts of a body when each pushes the other from it.

SHEAR STRESS:

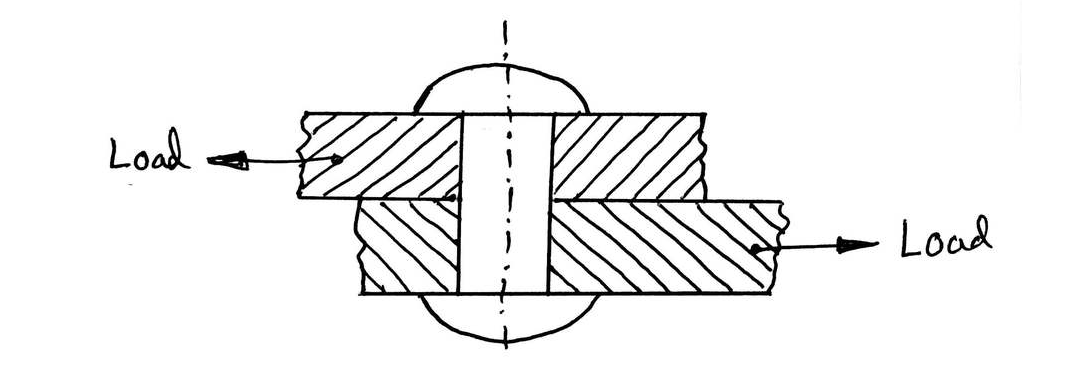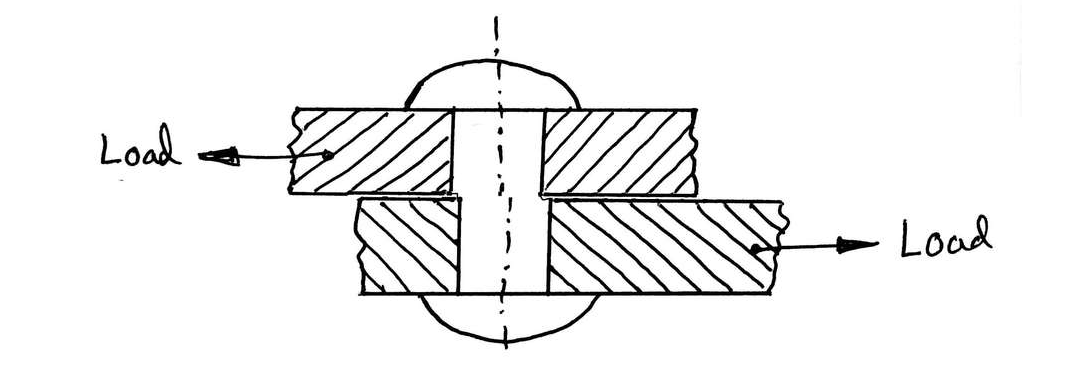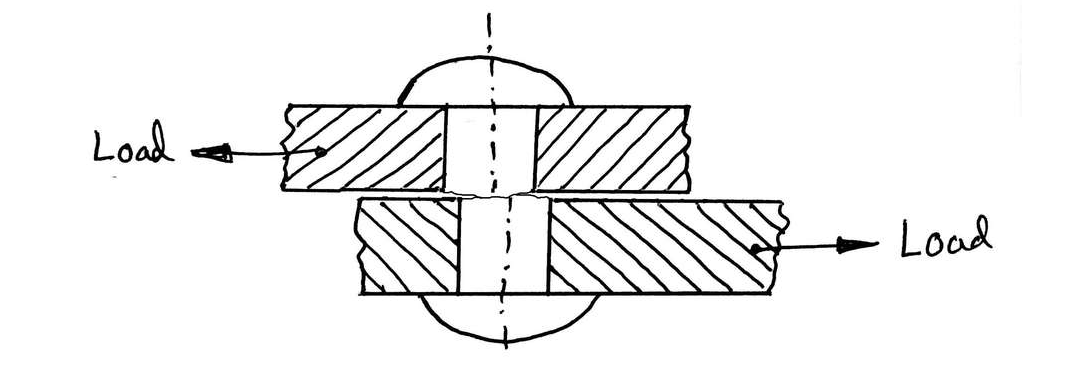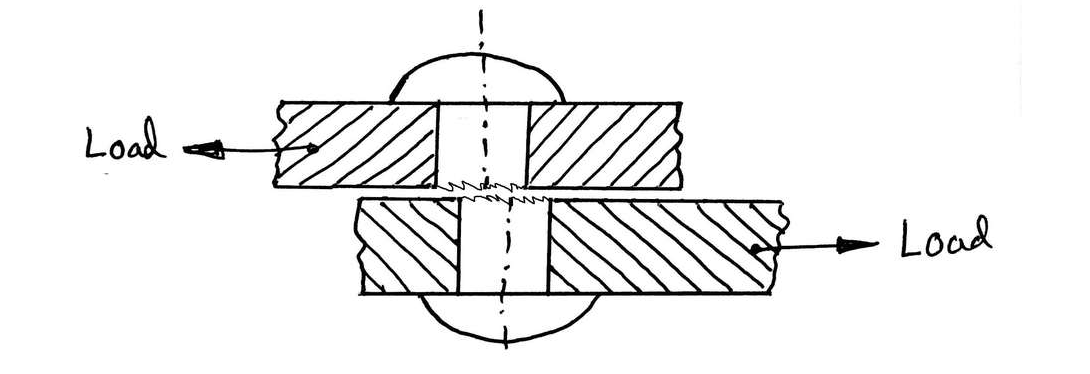
Shear stress is the one which acts parallel or tangential to the surface. Thus, shear stress exists between the parts of a body when the two parts exert equal and opposite forces on each other laterally in a direction tangential to their surface in contact.

UNITS OF STRESS:

Since normal stress is obtained by dividing the axial force by the cross-sectional area, it has units force per unit area. In S.I. units, the units of force is newton expressed by symbol N, and the area is expressed in square metres (m²). Hence the unit of stress is newtons per square metre ([frac up=”N” down=”m²“]) or Pascals.
However, newton is such a small unit of stress that it becomes necessary to work with large multiples. Due to this, force is generally expresses in terms of kilo-newton and mega-newton.

STRAIN:

When a prismatic bar is subjected to axial load, it undergoes a change in length. This change in length is called deformation.

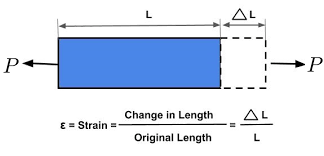
If the axial force is tensile, the length of the bar is increased while if the axial force is compressive, there is shortening of the length of the bar. This elongation or shortening is the cumulative result of the stretching of the material throughout the length of the bar.
The deformation per unit length of the bar is termed as strain.

Strain is the measure of the deformation caused due to external loading.

STRAIN, ε = [frac up=”Change in Length” down=”Original Length”] = [frac up=”ΔL” down=”L”]

TYPES OF STRAINS:

Tensile Strain
Compressive Strain
Shear Strain
Volumetric Strain

TENSILE STRAIN:

A piece of material, with uniform cross-section, subjected to a uniform axial tensile stress, will increase its length and this increment of length is the actual deformation of the material.

COMPRESSIVE STRAIN:

A piece of material, with uniform cross-section, subjected to a uniform axial compressive stress, will decrease its length and this decrement of length is the actual deformation of the material.

SHEAR STRAIN:

A piece of material, with uniform cross-section, subjected to a shear stress, will produce shear strain which is measured by the angle through which the body distorts.

VOLUMETRIC STRAIN:

It is defined as the ratio between change in volume and original volume of the body.

Volumetric Strain, ε_v= [frac up=”Change in Volume” down=”Original Volume”] = [frac up=”δV” down=”V”]

Since, strain is the deformation per unit length, it is a dimensionless quantity. Thus it has no units.

Equations of normal stress and strain can be used for loads of any magnitude and for any material. The principal requirement is that the deformation must be uniform, which in turn requires that the bar should be prismatic, the load act through the centroids of the cross-sections and the material be homogenous.