ANALYSIS OF BENDING EQUATION
Analysis of Bending Equation is done to derive various identities which are very helpful in selecting the material.
[frac up=”MR” down=”IN.A“] = [frac up=”σb” down=”y”] = [frac up=”E” down=”R”]
A = B = C
CASE I: A = B
[frac up=”MR” down=”IN.A“] = [frac up=”σb” down=”y”]
σb = [frac up=”MR” down=”IN.A“] . y ……(1)
This equation is used to determine the σb at any fibre on the plane of cross-section.
From equation 1 for a given cross-section of a beam, [frac up=”MR” down=”IN.A“] = constant
Therefore, σb ∝ y
Equation 1 is used to determine the bending stress σb developed at a fibre on the cross-section of beam when bending moment on that cross-section is known.
(σb)max = [frac up=”MR” down=”IN.A“] . ymax
(σb)max = [frac up=”MR” down=”IN.A/ymax “]
(σb)max = [frac up=”MR” down=”ZN.A“] ……(2)
Equation 2 is used to determine the maximum bending stress developed on the cross-section of the beam when bending moment acting on that cross-section is known.
where, ZN.A = Section modulus of cross-section of beam in mm3, it represents the strength of the section.
From equation 2 for a given cross-section of bending moment
(σb)max ∝ [frac up=”1″ down=”ZN.A“]
Best cross-section is the one which have more section modulus because Maximum Bending Stress (σb)max and Section Modulus, ZN.A are inversely proportional.
For a given cross-sectional area and bending stress, I-section is the best section.
ZN.A ↑ → σb ↓ → Chances of bending failures ↓
As Section Modulus increases the Bending Stress will decrease and chances if Bending Failure will decrease.
ymax = larger of ytop and ybottom
ytop and ybottom are same in case of square, rectangle and circle.
[frac up=”σb” down=”σbmax“] = [frac up=”y” down=”ymax“]
σb = (σb)max . [frac up=”y” down=”ymax“] ……(3)
Equation 3 is used to determine the Bending Stress,σb at any fibre.
[frac up=”σbTop” down=”σbBottom“] = [frac up=”yTop” down=”yBottom“]
For square, rectangle and circle the above mentioned ratio is 1.
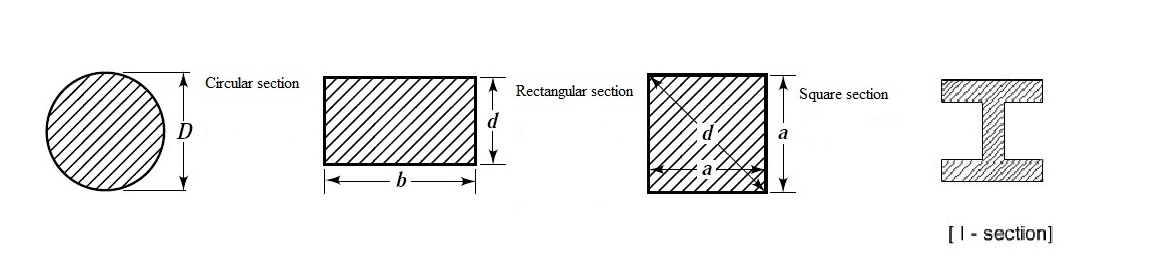
- Circular section is the worst section because it has least section modulus and the material is less at the extreme fibers as compared to the neutral axis.
- I-section is the best section because bending stress is maximum at the top and bottom ends therefore it is requested to provide more material at the top and bottom section and less material at neutral axis and in I-section all these conditions are satisfied.
- Square and Rectangular sections are uneconomical because in those sections same amount of material is provided from top and bottom.
- Section modulus not only depends on area, it also depends upon the disposition of area.
- A square with vertical and horizontal sides is economical than a square with horizontal and vertical diagonals.
- Circular hollow section is better than solid circular section for a given cross-sectional area.
- A rectangle with more depth is better than rectangle with more width and less depth for a given cross-sectional area.
SAFE CONDITION FOR DESIGN BASED ON STRENGTH CRITERION:
[(σb)max] ≤ σper
[frac up=”M” down=”ZN.A“] ≤ σper
M ≤ ZN.A . σper
MR = ZN.A . σper ……(4)
Equation 4 is used to compare the beams with respect to their moment of resistance or strength.
From equation 4, for a given material, MR ∝ ZN.A
As section modulus (ZN.A) increases, Moment of Resistance increases and chances of failure decreases.
- So from CASE I we got the following equations:
(σb)max = [frac up=”M” down=”ZN.A“]
Above mentioned equation is used for design purpose
σb = [frac up=”M . y” down=”IN.A“] or σb = (σb)max . [frac up=”y” down=”ymax“]
above mentioned equation is used for determining the bending stress at tinner fibre when bending stress at extreme fibre is known.
MR = ZN.A . σper
Above mentioned equation is used for comparing given different bars.
CASE II: B=C
[frac up=”σb” down=”y”] = [frac up=”E” down=”R”]
σb = [frac up=”E” down=”R”] . y ……(5)
(σb)max = [frac up=”E” down=”R”] . ymax ……(6)
When radius of curvature at neutral fibre is known than these equations are used.
From the above two equations we can conclude the following things:
- Material having less Modulus of Elasticity (E) and less ymax and more Radius of Curvature (R) should be used to reduce the Bending Stress (σb).
- That’s Why we use leather for belt instead of steel because it have less Modulus of Elasticity (E).
- Thickness of the belt should be less and width should be more to get less ymax. As we can see in flat belt.
- Pulleys with more radius should be used to increase Radius of Curvature (R).
- Thin and wider belts are preferable than thick and narrower belts for flat belt drive.
- For belts Moment of Resistance (MR) should be less because they need to be flexible.
- For beam Moment of Resistance (MR) should be high because they are need to be rigid.
CASE III: A = C
[frac up=”MR” down=”IN.A“] = [frac up=”E” down=”R”]
E . IN.A = MR . R = Flexural Rigidity
If R = 1 than E . IN.A = MR
Flexural Rigidity is defined as the amount of MR offered by the cross-section of a beam for a unit radius of curvature (R) of neutral fibre.
E . IN.A ↑ = MR ↑ = Slope and Deflection ↓ = Chances of Failure ↓
As flexural rigidity increases, the Moment of Resistance increases due to which slope and deflection decreases and thus chances of failure will also decrease.
- Section Modulus (Z) should be used in the design of beams based on strength criterion (for stress) whereas Flexural Rigidity should be used in the design of the beams based on Rigidity Criterion (for strain).
- Section Modulus (Z) represents the strength of the section. It depends upon the moment of inertia which again depends upon, not only on the total area of the cross-section but on the disposition of the area with respect to neutral axis.
RELATED VIDEO FOR ANALYSIS OF BENDING EQUATION: