The tendency of the forces is not only to move a body but also to rotate the body. This rotational tendency of a force is known as MOMENT.
It is the turning effect of a force, acting on a body about a hinged point.
The product of force and perpendicular distance from the point to the line of action of the force is called moment of a force about that point. Thus it depends on the following:
- Magnitude of the force.
- Perpendicular distance from the hinged point to the line of action of the force.
Consider a body nailed at a point O and acted by a force F. This force F tends to turn the body about O. This turning effect of the force F is called moment of the force. However, if the force is such that it passes through the point O, then it will not tend to rotate the bod but it will tend to move the body in a straight line.
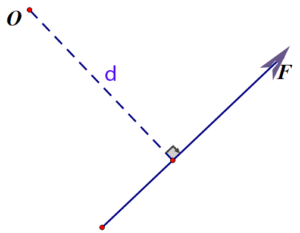
Magnitude of moment at O is, Mo = F x d
where d is the perpendicular distance of point O from the line of action of the force.
Moment of a force is a vector quantity
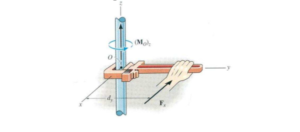
The direction of Mo will be obtained by using the right hand rule. To do this, fingers of the right hand are folded in such a way that they follow the sense of rotation. The thumb then points along the moment axis which gives the direction and sense of the moment.
UNITS:
In MKS unit = kg-m
In SI unit = N-m
CLOCKWISE AND ANTICLOCKWISE MOMENT:
According to the direction in which the force tends to rotate the body about a point or line, moments are classified as clockwise and anticlockwise.
If a force acting on a body has the tendency to rotate the body in clockwise direction, then the moment so produced is called CLOCKWISE MOMENT.
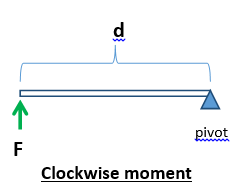
Moment at pivot = F x d (clockwise)
If a force acting on a body has the tendency to rotate the body in anticlockwise direction, then the moment so produced is called ANTICLOCKWISE MOMENT.
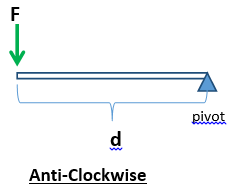
Moment at pivot = F x d (anticlockwise)
GEOMETRICAL INTERPRETATION OF MOMENT:
Let us consider a force F acting on a body and is represented by vector AB. Let O be the point about which moment of the force is to be calculated. Drop OC perpendicular to AB. Join OA and OB.
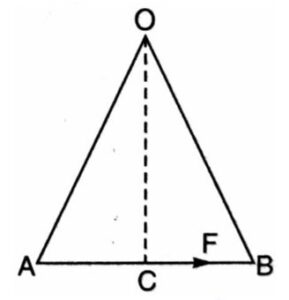
Now, moment of the force about O, Mo = F x OC
Mo = AB x OC
Mo = 2 x (1/2 x AB x OC)
Mo = 2 x Area of △OAB
Hence a moment of a force about a point is equal to twice of the area of the triangle so formed by taking the point as vertex of the triangle and the line as the base of the triangle.
PRINCIPLE OF MOMENT:
If a body is in equilibrium under the action of number of forces acting simultaneously on a body, then the algebraic sum of moments of all the forces about a point, in their plane is zero.
or
If a body is in equilibrium under the action of number of forces acting simultaneously on the body, then the algebraic sum of the clockwise moments of the forces about a point is equal to the sum of anticlockwise moments of the forces about the same point.
Diagram
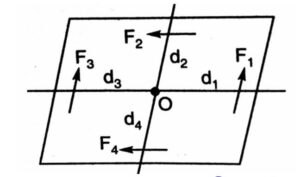
Let us consider four coplanar forces F1, F2, F3 and F4 acting on a body and the body is in equilibrium.
Let O be the point about which the body can rotate. Let d1, d2, d3 and d4 be the perpendicular distance of the point O form the line of action of the forces F1, F2, F3 and F4 respectively. Moment of the forces F1, F2, F3 and F4 about the point O is given:
Moment of force F1 = F1 x d1 (Anticlockwise)
Moment of force F2 = F2 x d2 (Anticlockwise)
Moment of force F3 = F3 x d3 (Clockwise)
Moment of force F4 = F4 x d4 (Clockwise)
The resultant of these moments will be equal to the algebraic sum of all the moments about O.
Resultant ∑M = F1d1 + F2d2 – F3d3 – F4d4
Since the body is in rotational equilibrium, according to the principle of moments, the resultant moment i.e. the algebraic sum of al the moments must be zero.
∑M = 0
F1d1 + F2d2 – F3d3 – F4d4
F1d1 + F2d2 = F3d3 + F4d4
Sum of anticlockwise moments = sum of clockwise moments
VARIGNON’S THEOREM:
It states that if a number of coplanar forces are acting on a body, then the algebraic sum of their moments about a point is equal to the moment of their resultant about the same point.
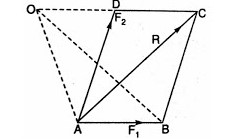
Let F1 and F2 be the two forces acting on a body whose resultant is F, then
Mo = r x F1 + r x F2
Mo = r(F1 + F2)
Mo = r x F
Let F1 and F2 be the two forces represented by the lines AB and AD. Let O be the point about which moment is to be taken. From O draw a line OC parallel to AB meeting AD at D. Join BC to complete the parallelogram. Now join the diagonal AC which gives the resultant R of the two forces. Join OA and OB.
From the figure,
area of △ ABC = area of △ ADC = area of △ AOB
(∵ These triangles lies on the same base and between two same parallel lines)
Now,
Moment of force F1 about O = 2 x area of △OAB
Moment of force F2 about O = 2 x area of △OAD
Moment of resultant force R about O = 2 x area of △OAC
Sum of moments of two forces about O = 2 x area of △OAB + 2 x area of △OAD
= 2 x area of △ADC + 2 x area of △OAD
= 2 x (area of △OAB + area of △OAD)
= 2 x area of △OAC
= Moment of the resultant force R about O
RELATED VIDEOS:
