LAW OF FORCES
CONDITIONS FOR EQUILIBRIUM:
When number of forces are acting on a body and the body is in equilibrium, this means there is no unbalanced force acting on the body i.e. the resultant of all the forces acting on the body is zero.
Analytical and Graphical conditions of equilibrium of coplanar concurrent forces are as under:
ANALYTICAL CONDITION:
- The algebraic sum of components of all the forces in the horizontal direction in their plane is zero, i.e., ∑H = 0.
- The algebraic sum of components of all the forces, in their plane, in the vertical direction is zero, i.e., ∑V = 0.
- The algebraic sum of moments of all the forces about a point in their plane is zero, i.e., ∑M = 0.
These are also called LAWS OF EQUILIBRIUM.
GRAPHICAL CONDITION:
If a force polygon of all the forces by choosing a particular scale is drawn then this polygon must close.
LAMI’S THEOREM:
It states that if three coplanar concurrent forces act on a body and keep the body in equilibrium, then each force is proportional to the sine of angle between the other two forces.
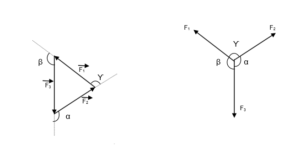
Consider three forces F1, F2 and F3 acting on a body at point O and the body is in equilibrium then according to Lami’s Theorem.
[frac up=”F1” down=”sin α”] = [frac up=”F2” down=”sin β”] = [frac up=”F3” down=”sin γ”]
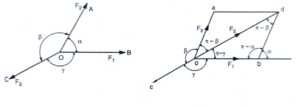
Proof: Let us consider the two forces F1 and F2 which are represented by the two sides ob and oa of the parallelogram obda. Then, the resultant of these two forces will be given by the diagonal of the parallelogram od in magnitude and direction. This means od should be equal to F3 but in opposite direction to OC as F1, F2 and F3 are in equilibrium.
Since ob || OB ; oa || OA || bd and do || OC
∴ ∠ AOC = ∠aoc = β
then ∠aod = π – β
∠ BOC = ∠boc = γ
∠bod = π – γ
∠ BOA = ∠boa = α
∠dbo = π – α
from triangle obd
[frac up=”ob” down=”sin (π – β) “] = [frac up=”bd” down=”sin (π – γ)”] = [frac up=”od” down=”sin (π -α)”]
[frac up=”F1” down=”sin α”] = [frac up=”F2” down=”sin β”] = [frac up=”F3” down=”sin γ”]
RELATED VIDEOS FOR LAMI’S THEOREM:
For More Information:- CLICK HERE
