GEOMETRICAL FIGURES
Quadrilateral is one of the plane geometrical figures bounded by four sides and four angles. Sum of the four angles in a quadrilateral is (interior angles) equal to 360°. The side joining opposite corners is called diagonal. To construct a quadrilateral out of four sides, four angles and two diagonals a minimum of five dimensions are required of which two must be sides. Quadrilaterals are also referred as Trapezium.
Types of quadrilaterals
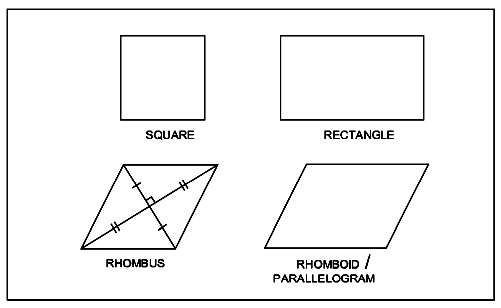
• Square
• Rectangle
• Rhombus
• Rhomboid / Parallelogram
Square: In a square all the four sides are equal and its four angles are at right angles. The two diagonals are equal and perpendicular to each other.
To construct a square we need to know length of the side or length of the diagonal.
Rectangle: In a rectangle, opposite sides are equal and parallel and all four angles are right angles.
To construct a rectangle we need to know the length two adjacent sides or diagonal and one side.
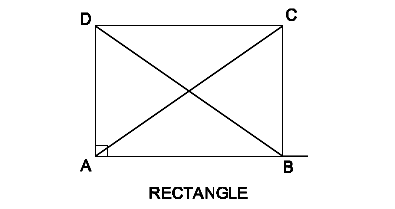
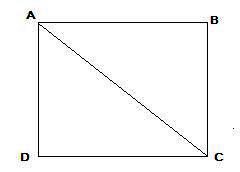
Figure shows a rectangle ABCD, Sides AB = DC and BC = AD. Diagonals AC and BD are equal. Diagonals are not bisecting at right angles.
Rhombus: In rhombus all the four sides are equal but only the opposite angles are equal. ABCD is the rhombus where AB = BC = CD = AD.
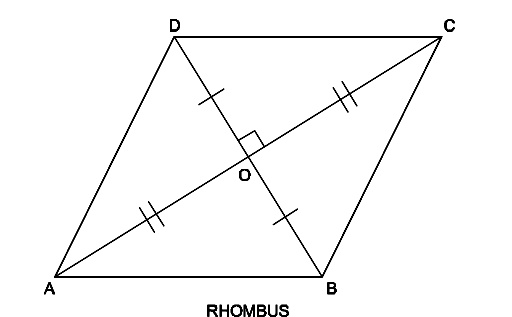
Angle ABC = Angle ADC and Angle BAD = Angle BCD.
Diagonals AC and BD are not equal but bisecting at right angles.
AO = OC and BO = OD.
To construct a rhombus we need to know two diagonals, one diagonal and an opposite angle or one side and its adjacent angle.
Rhomboid/Parallelogram: In a parallelogram opposite sides are equal and parallel. Opposite angles are also equal. Diagonals are not equal but bisect each other.
Parallelogram is also known as rhomboid. To construct a parallelogram we need (a) two adjacent sides and an angle between them or (b) one side, diagonal, and an angle between them or (c) two adjacent sides and perpendicular distance between the opposite sides.
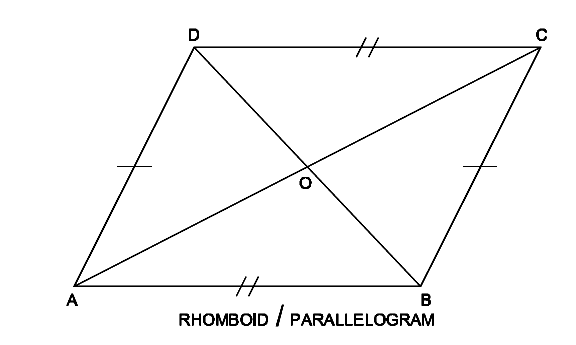
In the parallelogram ABCD, AB = DC; AD = BC
Angle DAB = angle DCB, angle ABC = angle ADC
Sides AB,CD and AD, BC are parallel.
Diagonals AC and BD are not equal but bisect at 0.
Circle: Circle is a plane figure bounded by a curve, formed by the locus of a point which moves so that it is always at a fixed distance from a stationery point the “Centre”.
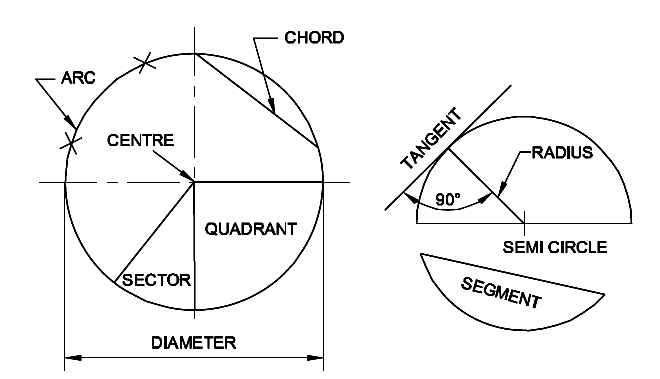
Radius: The distance from the centre to any point on the circle is called the “Radius”.
Diameter: The length of a straight line between two points on the curve, passing through the centre is called the “Diameter”. (D: Dia or d) It is twice the radius.
Circumference: It is the linear length of the entire curve, equal to πD .
Arc: A part of the circle between any two points on the circumference or periphery is called an ‘Arc’.
Chord: A straight line joining the ends of an arc is called the chord. (Longest chord of the circle is the diameter)
Segment: A part of the circle or area bound by the arc and chord is the segment of the circle.
Sector: It is the part of a circle bounded by two radii (plural of radius) meeting at an angle and an arc.
Quadrant: Part of a circle with radii making 90° with each other is a quadrant (one fourth of the circle).
Half of the circle is called as semi-circle.
Tangent: Tangent of a circle is a straight line just touching the circle at a point. It does not cut or pass through the circle when extended. The point where the tangent touches the circle is called the “point of tangency”. The angle between the line joining the centre to the point of
tangency and the tangent is always 90°.
Concentric circles: When two or more circles (drawn) having common centre, they are called concentric circles. Ball bearing is the best example of concentric circles.
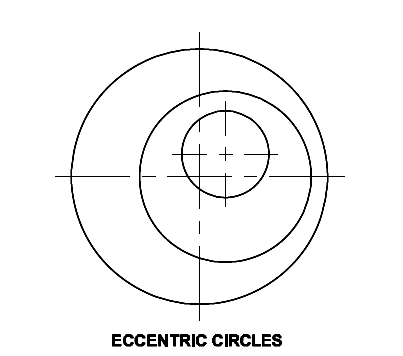
Eccentric circles: Circles within a circle but with different centres are called eccentric circles.