ELASTICITY AND PLASTICITY:
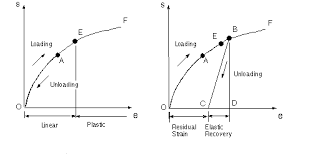
- When we apply a load to a tensile specimen so that the stress and strain go from O to A. When the load is removed, the material follows exactly the same curve back to the origin O. This property of a material, by which it returns to its original dimensions during unloading is called Elasticity.
- If we load the same material to a much higher level, so that the point B is reached. In this case when the unloading occurs the material follows line BC on the diagram. This unloading line is parallel to the initial portion of the loading curve i.e. line BC is parallel to a tangent to the stress- strain curve at O. When the point C is reached, the load has been entirely removed, but a residual strain or permanent strain remains in the material. This property of a material, by which it does not returns to its original dimension during unloading is called Plasticity.
CREEP:
- The stress-strain diagrams obtained from tension tests involving only static loading of the specimen. But some materials develop additional strains over long periods of time are said to creep.
- Creep is usually more important at high temperatures than at ordinary temperature. Hence it must be considered in the design of engines, furnace and other structures, that operates at elevated temperatures for long period of time.
- Materials such as steel, concrete and wood creep slightly even at atmospheric temperature. Therefore it is sometimes necessary to compensate for creep effects in ordinary structures.
- For example, creep of concrete can create waves in bridge decks because of sagging between supports. One remedy is to construct the deck with an upward camber, which is an initial deflection above the horizontal so that when creep occurs the spans lowers to the level position.
HOOKE’S LAW:
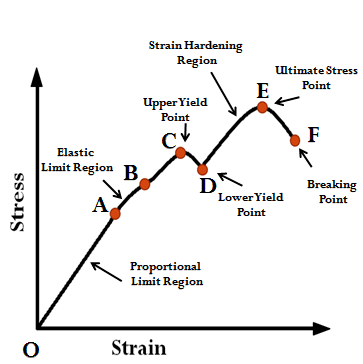
- The initial portion of stress-strain curve is straight. In this range the material behaves both elastically and linearly.
- When a material behaves elastically and also exhibits a linear relationship between stress and strain, it is said to be linearly elastic. This type of behavior is extremely important in engineering because many structures and many machines are designed to function at low level of stress in order to avoid permanent deformations from yielding.
- Linear elasticity is a property of many solid materials, including metals, wood, concrete, plastics and ceramics.
- Linear relationship between stress and strain for a bar in simple tension or compression can be expressed by the equation
σ ∝ ε
σ = E . ε
where E is the constant of proportionality (Modulus of Elasticity) which is defined as the intensity of stress that causes unit strain. Thus, modulus of elasticity (E) has the units same as units of stress.
E is the slope of the stress strain curve.
- Modulus of Elasticity (E) has large values for material that are stiff such as structural metals. E.g. Modulus of elasticity for steel is 200 GPA and thus strain will be less.
- Modulus of Elasticity (E) has small values for material that are flexible. E.g. Modulus of elasticity for wood is 11 GPA and thus strain will be more.
- Modulus of Elasticity has same unit as of stress i.e. [frac up=”N” down=”mm2“]
RELATED VIDEOS FOR HOOKE’S LAW: