STRENGTH OF MATERIALS- Elongation of Tapered Bar

TAPERED BAR:

A tapered bar or rod is basically a bar or rod with one of its end of larger diameter and other end of smaller diameter that means it tapers uniformly from one end to another end throughout the length.

ELONGATION OF TAPERED BAR UNDER AXIAL LOAD:

When a bar or rod with one of its end of larger diameter and other end of smaller diameter is subjected to an axial load then it is termed as elongation of tapered bar under axial load.

• When either the axial force or the cross-sectional area varies continuously along the axis of the bar, then equation δ =  [frac up=”PL” down=”AE”] is no longer suitable.

• Instead the elongation can be found by considering a differential element of the bar and then integrating over the entire length of the bar.

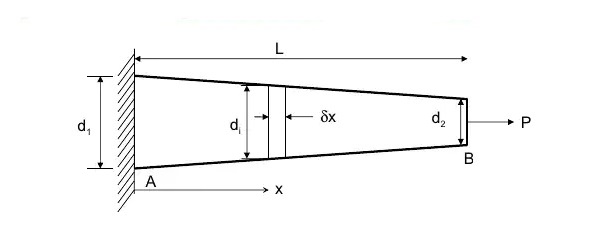
• Let us consider a uniformly tapering circular bar, subjected to an axial force (P), consider a section X-X of length δx and diameter di at a distance x from the end A.

• In order to compute the value of diameter of bar at a chosen location let us determine the value of K, from similar triangles.

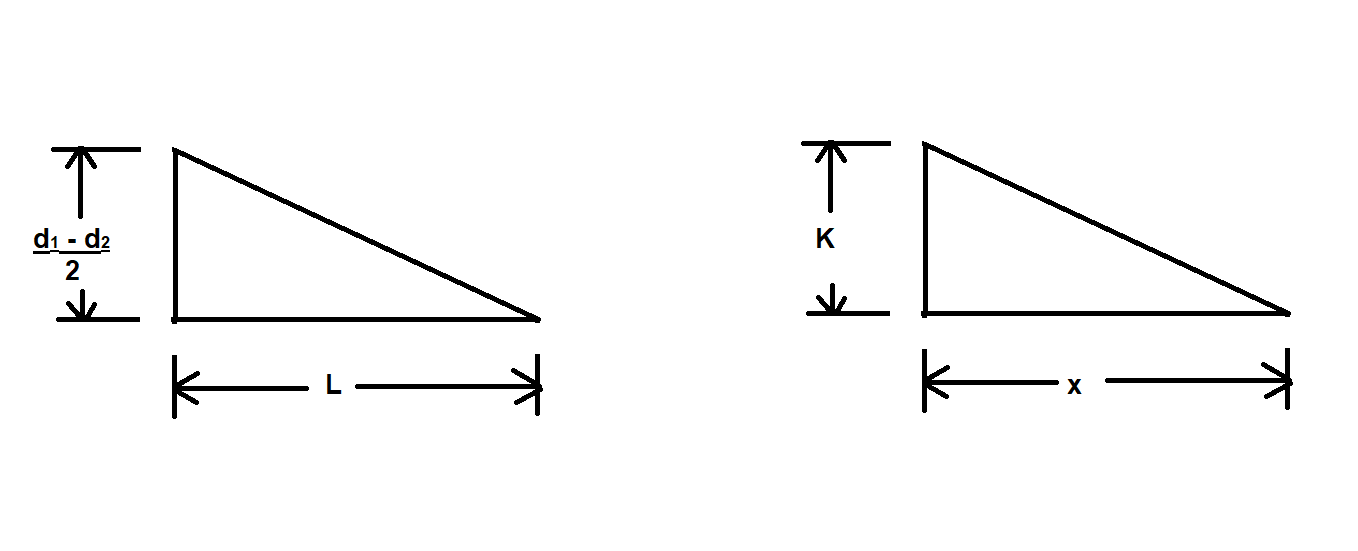
[frac up=”(d₁ – d₂)/2″ down=”L”] = [frac up=”K” down=”x”]

K = [frac up=”(d₁ – d₂) x” down=”2L”]

Diameter, d_i = d₁ + 2K = d₂ + [frac up=”(d₁ – d₂) x ” down=”L”]

Extension of the short length, δ_Δ = [frac up=”P . δ_x” down=”π/4 . d² . x . E”]

Hence extension of the whole length of the rod is

δ = ₀∫^L [frac up=”4 . P . δ_x” down=”π . (d₂ + 2K)² E”]

δ = [frac up=”4 . P” down=”π . E”]  ₀∫^L [frac up=”δ_x” down=”{d + (d₁ – d₂) k/L}²“]

After carrying out the integration we get,

δ = [frac up=”-4 . P . L” down=”π . E”] [ [frac up=”1″ down=”d₂“] – [frac up=”1” down=”d₁“] ]

δ = [frac up=”4 . P . L” down=”π . E . d₁ . d₂“]

 

When d₁ = d₂ = d, then δ = [frac up=”4 . P . L” down=”π . E . d . d”] = [frac up=”4 . P . L” down=”π . E . d²“] = [frac up=”P . L” down=”A . E “],  same as previous one.

Elongation of a prismatic bar under axial load is equal to elongation of an identical tapered bar under the same axial load. When diameter of prismatic bar is equal to the geometric mean of diameters of the tapered bar i.e. d = √d₁ . d₂

 

 

RELATED VIDEO FOR ELONGATION OF TAPERED BAR:

 

 

For More Information:- CLICK HERE