MOMENT
GEOMTERICAL INTERPRETATION OF MOMENT:
Let us consider a force F acting on a body and is represented by vector AB. Let O be the point about which moment of the force is to be calculated. Drop OC perpendicular to AB. Join OA and OB.
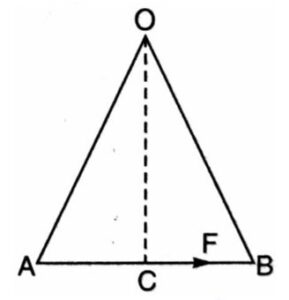
Now, moment of the force about O, Mo = F x OC
Mo = AB x OC
Mo = 2 x (1/2 x AB x OC)
Mo = 2 x Area of △OAB
Hence a moment of a force about a point is equal to twice of the area of the triangle so formed by taking the point as vertex of the triangle and the line as the base of the triangle.
PRINCIPLE OF MOMENT:
If a body is in equilibrium under the action of number of forces acting simultaneously on a body, then the algebraic sum of moments of all the forces about a point, in their plane is zero.
or
If a body is in equilibrium under the action of number of forces acting simultaneously on the body, then the algebraic sum of the clockwise moments of the forces about a point is equal to the sum of anticlockwise moments of the forces about the same point.
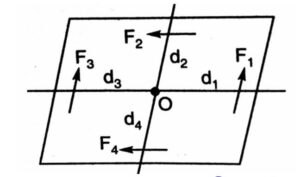
Let us consider four coplanar forces F1, F2, F3 and F4 acting on a body and the body is in equilibrium.
Let O be the point about which the body can rotate. Let d1, d2, d3 and d4 be the perpendicular distance of the point O form the line of action of the forces F1, F2, F3 and F4 respectively. Moment of the forces F1, F2, F3 and F4 about the point O is given:
Moment of force F1 = F1 x d1 (Anticlockwise)
Moment of force F2 = F2 x d2 (Anticlockwise)
Moment of force F3 = F3 x d3 (Clockwise)
Moment of force F4 = F4 x d4 (Clockwise)
The resultant of these moments will be equal to the algebraic sum of all the moments about O.
Resultant Moment ∑M = F1d1 + F2d2 – F3d3 – F4d4
Since the body is in rotational equilibrium, according to the principle of moments, the resultant moment i.e. the algebraic sum of al the moments must be zero.
∑M = 0
F1d1 + F2d2 – F3d3 – F4d4
F1d1 + F2d2 = F3d3 + F4d4
Sum of anticlockwise moments = sum of clockwise moments
VARIGNON’S THEOREM:
It states that if a number of coplanar forces are acting on a body, then the algebraic sum of their moments about a point is equal to the moment of their resultant about the same point.
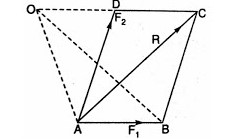
Let F1 and F2 be the two forces acting on a body whose resultant is F, then
Mo = r x F1 + r x F2
Mo = r(F1 + F2)
Mo = r x F
Let F1 and F2 be the two forces represented by the lines AB and AD. Let O be the point about which moment is to be taken. From O draw a line OC parallel to AB meeting AD at D. Join BC to complete the parallelogram. Now join the diagonal AC which gives the resultant R of the two forces. Join OA and OB.
From the figure,
area of △ ABC = area of △ ADC = area of △ AOB
(∵ These triangles lies on the same base and between two same parallel lines)
Now,
Moment of force F1 about O = 2 x area of △OAB
Moment of force F2 about O = 2 x area of △OAD
Moment of resultant force R about O = 2 x area of △OAC
Sum of moments of two forces about O = 2 x area of △OAB + 2 x area of △OAD
= 2 x area of △ADC + 2 x area of △OAD
= 2 x (area of △OAB + area of △OAD)
= 2 x area of △OAC
= Moment of the resultant force R about O
Related Videos for Principle of Moment:
