MOMENT
PARALLEL FORCES:
- The forces whose line of action are parallel to each other are called parallel forces.
- If the forces, having line of action parallel to each other, act in the same direction, then the forces are called Like Parallel Forces.
- If the forces, having line of action parallel to each other, act in the opposite directions, they are called Unlike Parallel Forces.
RESULTANT OF PARALLEL FORCES:
The resultant of parallel forces can be found by any of the following methods:
- Parallelogram law of forces method.
- Moments method.
- Graphical method.
-
MOMENTS METHOD
LIKE PARALLLEL FORCES: Let P and Q be the two parallel forces acting at point A and B. Thus their resultant R = P + Q acts in the direction of the forces. To find out the position of the resultant, take moment of the forces about the point C.
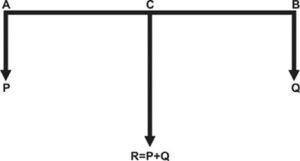
According to the principle of moments
P x AC = Q x BC
[frac up=”P” down=”BC”] = [frac up=”Q” down=”AC”]
UNLIKE PARALLEL FORCES: Let F1 and F2 (F2>F1) be the two forces acting at points A and B. Thus their resultant R = F2 – F1, acts in the direction of the greater force F2. Let the resultant force R be acting at point C situated outside AB.
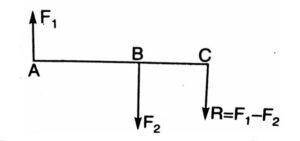
Taking moment of all the forces about point C.
F1 x AC = F2 x BC
[frac up=”F1” down=”BC”]= [frac up=”F2” down=”AC”]
-
GRAPHICAL METHOD
Consider a number of parallel forces (say three like parallel forces) P1, P2 and P3 whose
resultant is required to be found out as shown in figure
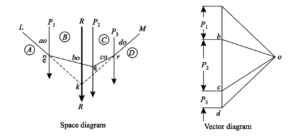
First of all, draw the space diagram of the given system of forces and name them according to Bow’s notations as shown in Fig. 4.6 (a). Now draw the vector diagram for the given forces as shown in Fig. and as discussed below :
1. Select some suitable point a, and draw ab equal to the force AB (P1) and parallel to it to some suitable scale.
2. Similarly draw bc and cd equal to and parallel to the forces BC (P2) and CD (P3) respectively.
3. Now take some convenient point o and joint oa, ob, oc and od.
4. Select some point p, on the line of action of the force AB of the space diagram and through it draw a line Lp parallel to ao. Now through p draw pq parallel to bo meeting the line of action of the force BC at q.
5. Similarly draw qr and rM parallel to co and do respectively.
6. Now extend Lp and Mr to meet at k. Through k, draw a line parallel to ad, which gives the required position of the resultant force.
7. The magnitude of the resultant force is given by ad to the scale.
RELATED VIDEOS:
