STRENGTH OF MATERIALS- Thermal Stresses and Strains

THERMAL STRESSES AND STRAINS

• If the temperature of a body is lowered or raised its dimensions will decrease or increase correspondingly. If these changes, however, are checked the stresses thus developed in the body are called temperature stresses and corresponding strains are called temperature strains.

• If the object is subjected to uniform changes in temperature, the sides of the object will change. If “α” is the coefficient of thermal expansion or contraction, the uniform thermal strain is given by

 ε_t = α . (t₂ – t₁)
or
ε_t = α . Δt

where,  Δt = (t₂ – t₁) = Change in temperature

• Consider a bar of length L, subjected to uniform increase in temperature (Δt), the bar being free to expand. Then the increase in the length of the bar. Then the increase in the length of the bar is,

ε_t . L = α . Δt . L

• Conditions for Thermal Stress
  • Thermal gradient must be there
  • Expansion or contraction due to thermal gradient is restricted partially or fully.

Total stress developed in a component = Mechanical Stress + Thermal Stress

In presence of thermal variation when dimensional stability is required during the functionality of a component, INVAR (Nickel and Steel Alloy) is selected as a material for that component because it have least coefficient of thermal expansion.

α_Invar = 1.2 x 10^-6 / °C

α_Diamond = 1.1 x 10^-6 / °C

Diamond is not used because of its high cost.

Coefficient of thermal expansion for various common materials:

α_Steel = 12 x 10^-6 / °C

α_Copper = 16 x 10^-6 / °C

α_Brass = 20 x 10^-6 / °C

α_Aluminum = 23 x 10^-6 / °C

CASE I: FREE EXPANSION

In this case, when the bar is heated or cooled than the bar is free to expand.

Change in dimension along x-axis, (𝛿_th)_x = α . ΔT . L

Change in dimension along y-axis, (𝛿_th)_y =  α . ΔT . d

Change in dimension along z-axis, (𝛿_th)_z = α . ΔT . d

Thermal Strain, (ε_th)_x = (ε_th)_y = (ε_th)_z = α . ΔT

Thermal Stress, (σ_Th)_x = (σ_Th)_y = (σ_Th)_z = 0

On heating the bar its length will increase and in this case the expansion of the bar is not restricted so no Thermal Stress will be there.

CASE II: COMPLETELY RESTRICTED EXPANSION IN ONE DIRECTION

In this case, the bar is not allowed to expand when there is expansion or contraction due to change in temperature.

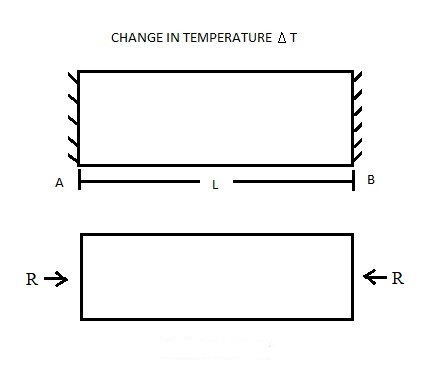
Total change in length= Change in length due to Thermal Stress + Change in length due to Normal Stress = 0

(𝛿_L)_Total = (𝛿_Th) + (𝛿_Al) = 0

α . ΔT . L – RL/AE = 0

α . ΔT . L = RL/AE

R = α . ΔT . A . E

Thermal Stress, σ_Th = R/A = α . ΔT . E

• When temperature rises, σ_Th is compressive in nature.
• When temperature falls, σ_Th is tensile in nature.

From the above equation of thermal stress it can be concluded that the thermal stress is independent of the dimension of the member.

CASE III: PARTIALLY RESTRICTED EXPANSION

In this case, the bar is allowed to expand partially.

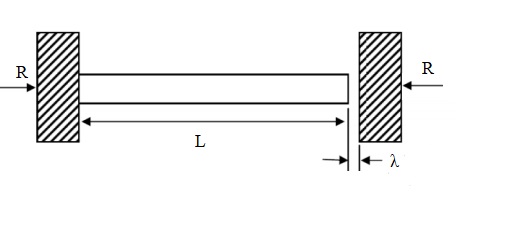
Total change in length= Change in length due to Thermal Stress + Change in length due to Normal Stress = λ

(𝛿_L)_Total = (𝛿_Th) + (𝛿_Al) = λ

α . ΔT . L – RL/AE = λ

RL/AE = α . ΔT . L – λ

Thermal Stress, σ_Th = (α . ΔT . L - λ/L) . E

Thermal Stress, σ_Th = (𝛿_Th - λ/L) . E

where, λ = Expansion permitted by the flexible supports

RELATED VIDEOS: