LAW OF FORCES

RESULTANT FORCE:

When two or more forces acting on a body are replaced by a single force, the effected produced by the force is same as that of the forces. Then that single for is called resultant force of the forces.

A resultant force is a single force which can replace two or more forces and produce same effect on the body as the forces.

METHODS OF FINDING THE RESULTANT FORCES:

Parallelogram law of forces

Triangle law of forces

Polygon law of forces

TRIANGLE LAW OF FORCES:

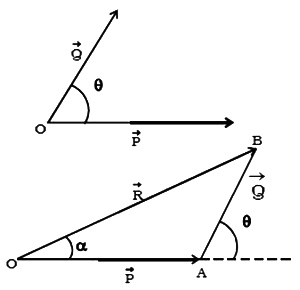
Triangle law of forces states that if two concurrent forces are acting simultaneously on a body and are represented in magnitude and direction by the sides of a triangle taken in order, then the third side of the triangle represents their resultant of the forces in magnitude and direction taken in opposite order.

GRAPHICAL METHOD:

Draw vector OA and AB to some scale to represent P and Q respectively. Then close the triangle by joining OB. Measure OB and convert it into force unit by using the same scale. This gives the value of R.

ANALYTICAL METHOD:

Consider the triangle OAB, θ is the angle between P and Q and α be the angle between P and R.

∠BAC = θ and ∠BOC = α
∠OBA = θ – α

Using the sine rule, we get

[frac up=”P” down=”sin (θ – α)”] = [frac up=”Q” down=”sin α”] = [frac up=”R” down=”sin (180°- θ)”]

[frac up=”P” down=”sin (θ – α)”] = [frac up=”Q” down=”sin α”] = [frac up=”R” down=”sin θ”]

POLYGON LAW OF FORCES:

Polygon law of forces states that if number of coplanar concurrent forces acting simultaneously on a body be represented in magnitude and direction by the sides of a polygon taken in order, then the closing side of the polygon will represent force in magnitude and direction, taken in opposite order.

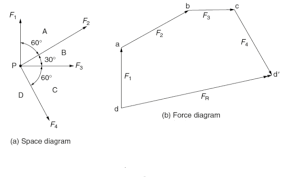
Let us consider a body in which four coplanar forces are acting as sown in figure. The resultant can be found bot graphically and analytically.

GRAPHICAL METHOD:

Draw vectors da, ab, bc and cd to some scale to represent forces F1, F2, F3 and F4 simultaneously. The vectors are drawn parallel to the forces starting from a point.

Then close the polygon by joining dd’. Measure dd’ and convert it into the force unit using the same scale. This gives the value of Resultant.

If the forces F1, F2, F3 and F4 acting simultaneously on a particle be represented in magnitude and direction by the sides da, ab, bc and cd of a polygon respectively, their resultant, FR is represented by the closing side dd’ taken in opposite order.

ANALYTICAL METHOD:

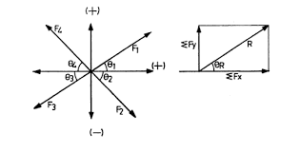
Let four force F1, F2, F3 and F4 acting at a point O making angles θ1, θ2, θ3 and θ4 with the X-axis respectively. Let R be the resultant force acting at angle θ with the X-axis.

Resolving the forces along the X-axis, i.e. horizontally, we get
ΣFx = F1 cos θ1 – F2 cos θ2 – F3 cos θ3 + F4 cos θ4

Resolving the forces along the Y-axis, i.e. vertically, we get
ΣFy = F1 sin θ1 + F2 sin θ2 – F3 sin θ3 – F4 sin θ4