LAW OF FORCES

RESULTANT FORCE:

When two or more forces acting on a body are replaced by a single force, the effected produced by the force is same as that of the forces. Then that single for is called resultant force of the forces.

A resultant force is a single force which can replace two or more forces and produce same effect on the body as the forces.

METHODS OF FINDING THE RESULTANT FORCES:

• Parallelogram law of forces

• Triangle law of forces

• Polygon law of forces

PARALLELOGRAM LAW OF FORCES:

It states that if two concurrent forces, acting simultaneously on a body be represented in magnitude and direction by the two sides of a parallelogram then their resultant may be represented in magnitude and direction by the diagonal of the parallelogram, drawn from the same point.

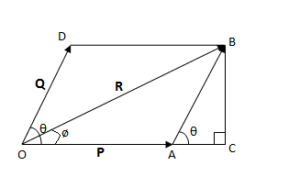
The value of R can be determined either graphically or analytically.

GRAPHICAL METHOD:

First choose a convenient scale to convert force unit into length unit. Then draw vector OA and OD to represent P and Q in magnitude and directions. Complete the parallelogram OABD by drawing DB parallel to OA and AB parallel to OD. Join OB and measure the length. Convert the length into force by suing the same scale to get the value of R.

ANALYTICAL METHOD:

Drop perpendicular BC to OA produced
Now from the figure,
∠AOD =  ∠CAB

Consider the right angled triangle ACB

Then, CB = AB sin θ = Q sin θ
AC = AB cos θ = P cos θ

Now from right angled triangle OCB

OB² = CB² + OC²
OB² = CB² + (OA + AC)²
OB² = CB² + OA² +AC² + 2 x OA x OC
R² = Q² sin² θ + P² + Q² cos² θ + 2 x P x Q x cos θ
R² = P² + Q² (sin² θ + cos² θ ) + 2.P.Q.cos θ
R² = P² + Q² + 2.P.Q.cos θ
R   = √(P² + Q² + 2.P.Q.cos θ)

Above equation gives the magnitude of R.

Let ∠BOA = ϕ i.e. R makes an angle ϕ with P

tan ϕ = CB/OC = CB/(OA + OC)

tan ϕ = Q sin θ/(P + Q cos θ)

ϕ = tan ^–1 Q sin θ/(P + Q cos θ)

The value of  ϕ gives the direction which the resultant R makes with the force P.

SPECIAL CASES:

Case 1: If θ = 0° i.e. when P and Q are acting on the same straight line and in the same direction. Then equation becomes

R   = √(P² + Q² + 2.P.Q.cos θ)
R   = √(P² + Q² + 2.P.Q)           (∵ cos 0° = 1)
R   = P + Q

i.e. when two forces are acting in the same line and in the same direction then the resultant of the two forces can be obtained by adding the two forces.

Case 2: If θ = 90° i.e. when P and Q are acting at right angles, then
R   = √(P² + Q² + 2.P.Q.cos θ)
R   = √(P² + Q²)           (∵ cos 90° = 0)

Case 3: If θ = 180° i.e. when P and Q are acting on the same straight line but in the opposite direction, then
R   = √(P² + Q² + 2.P.Q.cos θ)
R   = √(P² + Q² – 2.P.Q)           (∵ cos 180° = -1)
R   = P – Q

i.e. when two forces are acting in the same line but in the opposite direction then the resultant of the two forces can be obtained by subtracting minor force with the major force and the resultant will act in the direction of the major force.

RELATED VIDEOS: